《漢書·律曆志》筆記(4):統術(附歲術)
統術是三統曆的基本曆法計算方法,可以用來計算一年在三統中的位置,該年天正月朔日的干支名稱(也就是日名)、冬至日和其他所有節氣的日名,以及本年是否需要置閏和在哪一個月置閏。除此之外,統術還包括計算天正月朔日日月所在星度、月食時刻等方法。三統曆以建子月,也就是夏正十一月爲曆法的起始,也是每年的第一個月,稱之爲天正。《律曆志》說:
其於三正也,黃鐘子為天正,林鐘未之衝丑為地正,太族寅為人正。
天正建子,以夏正十一月爲正月;地正建丑,以夏正十二月爲正月;人正建寅,以夏正正月爲正月。所以地正比天正晚一個月,人正比天正晚兩個月。但是除了在推天正、地正、人正中,一般都只以天正建子、夏正十一月爲一年的第一個月。所謂朔日,就是建子月的第一天。求閏月,也是從建子月開始。例如上一部分所舉的十九年一章中的第三年有閏九月,這個閏九月是從建子月,也就是夏正十一月開始數的。
統術各部分其實都是以已知數推求未知數的題目;所用數據有兩項,一項是常數,也就是統母中所列的數據,另一項是已知數,也就是由統術其他部分得出的結果。最基本的已知數其實只有一個數值,就是所求年距太極上元的年數,其他已知數都可以從該數求出。下表列出統術各項計算所用常數(統母)、已知數與所求數。其中太極上元以來年數爲 $x$,入統歲數爲 $n$。
| 統術 | 所用常數 | 已知數 | 所求數 | 公式 |
|---|---|---|---|---|
| 推日月元統 | 元法、統法 | 太極上元以來年數 | 統數,入統歲數 | $x \ \mathbf{mod}\ \text{元法}\ \mathbf{mod}\ \text{統法}$ |
| 推天正 | 章月、章歲 | 入統歲數 | 積月、閏餘 | $\text{積月} = n \times \text{章月} \ \mathbf{div}\ \text{章歲}$\ $\text{閏餘} = n \times \text{章月} \ \mathbf{mod}\ \text{章歲}$ |
| 推正月朔 | 月法、日法、統首日 | 積月 | 積日、小餘、朔日干支 | $\text{積日}=\text{積月} \times \text{月法} \ \mathbf{div}\ \text{日法}$\ $\text{積日小餘}=\text{積月} \times \text{月法} \ \mathbf{mod}\ \text{日法}$\ $\text{積日大餘}=\text{積日} \ \mathbf{mod}\ \text{60}$ |
| 推閏餘 | 章中 | 閏餘 | $(章中 - 12 \times 閏餘) \ \mathbf{mod}\ 7 + 1$ | |
| 推冬至 | 策餘、統法、統首日 | 入統年 | 冬至大餘、小餘、干支 | $大餘 = (入統年 \times 策餘) \ \mathbf{div}\ 統法$\ $小餘 = (入統年 \times 策餘) \ \mathbf{mod}\ 統法$ |
| 推五行 | 統法(歲) | |||
| 推合晨所在星 | 統法、周天 | 積日、積日小餘 | 合晨度 | |
| 推其日夜半所在星 | 章歲、統法 | 月小餘(積日小餘)、合晨度 | 日夜半星度 | |
| 推其月夜半所在星 | 月周、統法 | 月小餘(積日小餘)、合晨度 | 月夜半星度 | |
| 推諸加時 | 小餘、各盈分母 | 加辰 | ||
| 推月食 |
下面這張圖展示了統術所用的已知數、統術所求的未知數,以及相互之間的關係。其中方框中的是統術的名稱,而橢圓中的是統術所用的已知數或所求的未知數。
統術部分只給出最終的公式計算方法,而略過了計算原理與中間步驟,爲求明晰,下面的解釋列出所有演算步驟。
推日月元統
推日月元統,置太極上元以來,外所求年,盈元法除之,餘不盈統者,則天統甲子以來年數也。盈統,除之,餘則地統甲辰以來年數也。又盈統,除之,餘則人統甲申以來年數也。各以其統首日為紀。
推日月元統是通過本年距上元年數計算出本年在三統中屬於第幾元第幾統第幾年。三統曆一元 4617 年,即元法;分一元爲天統甲子、地統甲辰、人統甲申,即三統,每統 1539 年。
假設本年距上元年數 $x$,則:
本年所在元數:$$x\ \mathbf{div}\ 4617$$ 本年所在統數:$$x\ \mathbf{mod}\ 4617\ \mathbf{div}\ 1539$$ 本年所在統數內年數:$$x\ \mathbf{mod}\ 4617\ \mathbf{mod}\ 1539$$
用 python 寫出來就是:
n % 4617 // 1539 # 本年所在統數,0 天統,1 地統,2 人統
n % 4617 % 1539 # 本年所在統數內年數
例如,伐紂之年距上元 142109 年,該年所在元數爲 $142109 \ \mathbf{div}\ 4617 = 30$,所在統數爲 $142109 \ \mathbf{mod}\ 4617 \ \mathbf{div}\ 1539 = 3$,也就是人統甲申;該年在人統年數爲 $142109 \ \mathbf{mod}\ 4617 \ \mathbf{mod}\ 1539 = 521$,也就是本年入人統甲申第 521 年。
推天正、地正、人正
推天正,以章月乘人[入]統歲數,盈章歲得一,名曰積月,不盈者名曰閏餘。閏餘十二以上,歲有閏。求地正,加積月一;求人正,加二。
根據入統年數計算天正、地正、人正。其實就是計算本年有沒有閏月。如果閏餘大於 12,本年就有閏月。三統曆一章 19 歲,一章總共 $19 \times 12 + 7 = 235$ 個月,每年 $235 \div 19 = \frac{235}{19} = 12 \frac{7}{19}$ 個月。假設入統年數爲 $n$,則該年積月 $n \times 12 \frac{7}{19}$,將這個數化爲帶分數,帶分數的分子部分稱之爲閏餘。如果該年閏餘大於 12,則本年需要置閏。寫成算式就是:
入統年數 $n$ 乘以一年月數,化爲帶分數:
$$ \begin{align*} &n \times \frac{235}{19}\\ =& (n \times 235)\ \mathbf{div}\ 239 \frac{(n\times235)\ \mathbf{mod}\ 19}{19} \end{align*} $$
$$$$
寫成代碼就是:
n * 235 // 19 # 積月
n * 235 % 19 # 閏餘
由於天正以建子(十一月)爲一年起點,所以如果用的是地正建丑,以十二月爲一歲起點,那積月就要加一;而人正建寅,以正月爲起點,積月要加二。
已知伐紂之年爲人統甲申第 521 年,則本年積月 $521 \times 235 \ \mathbf{div}\ = 6443$ 月,閏餘 $521 \times 235 \ \mathbf{mod}\ 19 = 18$,閏餘大於 12,所以本年是閏年。
推正月朔、求其次月、求(正月)弦、望
推正月朔,以月法乘積月,盈日法得一,名曰積日,不盈者名曰小餘。小餘三十八以上,其月大。積日盈六十,除之,不盈者名曰大餘。數從統首日起,算外,則朔日也。
求其次月,加大餘二十九,小餘四十三。小餘盈日法得一,從大餘,數除如法。求弦,加大餘七,小餘三十一。求望,倍弦。
這一段分爲兩部分。第一部分推正月朔是由已知年數的總月數(積月)求該年天正月朔日(建子月初一)的干支名稱。積月已經在上一部分推天正求出了。積月乘以一月日數 $29 \frac{43}{81}$,將這個數化爲帶分數,帶分數的整數部分就是積日,即入統以來總共有多少天。再將積日除以干支週期數 60,用所得小餘從統首日數起就是本年正月朔日所在干支。
上一部分已經算出積月,即 $n \times 235 \ \mathbf{div}\ 19$,設積月爲 $j$,這裏用積月算出積日和積日小餘,再用積日除以干支週期,所得餘數就是積日大餘。
$$ \begin{align*} \text{積月} \times \frac{\text{月法}}{\text{日法}} &=j \times \frac{2392}{81}\\ &= ((j \times 2392)\ \mathbf{div}\ 81) \frac{j \times 2392 \ \mathbf{mod}\ 81}{81}\\ &= \text{積日} \frac{積日小餘}{81}\\ \text{積日大餘}&=\text{積日}\ \mathbf{mod}\ 60 \end{align*} $$
寫成代碼就是:
# 入統第 n 年的積日,tongshouri 爲統首日干支,天統甲子,地統甲辰,人統甲申
def tuiZhengyueshuo(n, tongshouri):
jiri = ((n * 235 // 19)
* 2392).numerator // 81 # 入統第 n 年積日
jirixiaoyu = ((n * 235)// 19
* 2392) % 81 # 積日小餘
jiridayu = jiri % 60 # 積日大餘
# 本年朔旦干支
shuoriGanzhi = ganzhi[ganzhi.index(tongshouri) + jiridayu]
return jiri, jirixiaoyu, shuoriGanzhi
伐紂入人統甲申 521 年,該年積日 190267 日,天正月朔日爲辛卯日。
第二部分,求其次月。因爲推正月朔已經求出當月的積日大餘與積日小餘,所以這裏再加上一個月的月長。如果本月的積月小餘加 43 大於 81,就說明下月大,次月大餘要加一;否則次月小。
$$ \begin{align*} \text{次月大餘} &=\text{積日大餘} + 29 + (\text{積日小餘} + 43)\ \mathbf{div}\ 81\\ \text{次月小餘} &=(\text{積日小餘} + 43)\ \mathbf{mod}\ 81 \end{align*} $$
自本月朔日到上弦日,爲一月的四分之一,也就是 $29 \frac{43}{81} \div 4 = 7 \frac{31}{81}$;而朔日到望日就是一月的一半,即 $29 \frac{43}{81} \div 2 = 14 \frac{62}{81}$。要求本月的弦或望只要用本月積日大小餘分別加上相應的弦望大小餘就可以了。
$$ \begin{align*} \text{弦日大餘}&=\text{積日大餘} + 7\\ \text{弦日小餘}&=\text{積日大餘} + 31\\ \text{望日大餘}&=\text{積日大餘} + 14\\ \text{望日小餘}&=\text{積日大餘} + 62 \end{align*} $$
推閏餘所在
推閏餘所在,以十二乘閏餘,加(十)[七]得一。盈章中,數所得,起冬至,算外,則中至終閏盈。中氣在朔若二日,則前月閏也。
這一段求所求年如有閏月,當置於哪月。在推天正部分已經求出本年的閏餘 $n \times 235 \ \mathbf{mod}\ 19$,閏餘如果大於 12,本年就要置閏。但是閏月置於哪個月呢?三統曆將閏月置於無中氣之月。
一年有二十四個節氣,其中十二個中氣。一年的長度以月份來計算就是 $12 \frac{7}{19}$ 個月,那一個中氣平均長度就是 $12 \frac{7}{19} \div 12 = 12 \frac{7}{19 \times 12}$ 個月。也就是說,每過一個月,中氣就過 $12 \frac{7}{19 \times 12} = \frac{235}{228}$。一個月的長度當然是 1,那者一個月過了之後,就會餘下 $\frac{235}{228} - 1 = \frac{7}{228}$ 個中氣。幾個月過去,中氣比一個月長的部分不斷累積,最終就會超過一個月的長度。當中氣和月長的差距超過一月時,下個月就沒有中氣,閏月就設置在這個月。
上面推天正已經求出閏餘,閏餘以 19 爲分母。設閏餘爲 $u$,
$$ \begin{align*} \text{一月長}&=1\\ \text{一中氣長}&= \text{一年月長} \div \text{一年中氣數}\\ &=12 \frac{7}{19} \div 12\\ &= \frac{235}{228}\\ \text{中氣長}-\text{月長}&=\frac{235}{228} - 1\\ &=\frac{7}{228}\\ \text{m 月之後中氣剩餘}&= \frac{7m}{228}\\ \text{加上本年閏餘}\frac{u}{19}&=\frac{u}{19} + \frac{7m}{228}\\ &=\frac{12u + 7m}{228}\\ \text{當中氣累計剩餘超過}\ &228\ \text{時:}\\ 12 u + 7m &\geq 228\\ \text{無中氣之月}&=(228 - 12 u)\ \mathbf{div}\ 7 + 1 \text{, 如果 } 12u + 7m \gt 228\\ &=(228 - 12 u)\ \mathbf{div}\ 7 \text{, 如果 } 12u + 7m = 228 \end{align*} $$
注意,這裏算出來的無中氣之月是自建子月數的,如果是 2,那就是建子月之後兩個月閏月,就是建寅月閏月。前面已經說過,十九年一章中設置閏月的順序和時間都是固定的。在上一部分“三統曆算法的基本思路”中,已經列出來一章閏月的順序,這裏再列一遍:
| 年份 | 月份 |
|---|---|
| 第 3 年 | 閏九月 |
| 第 6 年 | 閏六月 |
| 第 9 年 | 閏二月 |
| 第 11 年 | 閏十一月 |
| 第 14 年 | 閏七月 |
| 第 17 年 | 閏四月 |
| 第 19 年 | 閏十二月 |
推冬至、八節、二十四氣
推冬至,以(算)[策]餘乘(人)[入]統歲數,盈統法得一,名曰大餘,不盈者名曰小餘。除數如法,則所求冬至日也。
求八節,加大餘四十五,小餘千一百。求二十四氣,三其小餘,加大餘十五,小餘千一十。
推中部二十四氣,皆以元為法。
這一段是根據入統年數求該年冬至日的干支。三統曆一年有 $365 \frac{385}{1539}$ 天,減去干支週期 60 的倍數 360,剩下 $5 \frac{385}{1539}$ 天,將這個數化爲帶分數 $\frac{8080}{1539}$,分子部分就是策餘。用策餘乘以入統歲數 $n$,以所得數除以統法,化爲帶分數,整數部分爲大餘1,分子部分爲小餘。再算出大餘除以干支週期 60 的餘數。從入統首日干支數起,就是冬至日的干支。寫成公式就是:
策餘乘以入統歲數:
$$ \begin{align*} \frac{\text{策餘}}{\text{統法}} \times \text{入統歲數}&= \frac{8080}{1539} \times n\\ &= (n \times 8080 \ \mathbf{div}\ 1539) \frac{n \times 8080 \ \mathbf{mod}\ 1539}{1539} \\ &= \text{大餘} \frac{\text{小餘}}{1539}\\ \text{大餘}\ &= n \times 8080 \ \mathbf{div}\ 1539\\ \text{小餘}\ &= n \times 8080 \ \mathbf{mod}\ 1539\\ \end{align*} $$
大餘除以干支週期的餘數:
$$\text{干支序數} = \text{大餘} \ \mathbf{mod}\ 60 + \text{入統首日干支序數}$$
寫成代碼就是:
def tuiDongzhi(n, tongshouri):
dongzhiDayu = n * 8080 // 1539
dongzhiXiaoyu = n * 8080 % 1539
dongzhiXushu = dongzhiDayu % 60
dongzhiGanzhi = ganzhi[ganzhi.index(tongshouri) + dongzhiXushu]
return dongzhiDayu, dongzhiXiaoyu, dongzhiGanzhi
伐紂之年入人統甲申 521 年,該年大餘爲 $521 \times 8080 \ \mathbf{div}\ 1539 = 2735$,大餘除以干支週期的餘數是 $2735 \ \mathbf{mod}\ 60 = 35$。從入統首日干支數起,甲申在干支表中的序數是 20,伐紂之年冬至干支的序數就是 $20 + 35 = 55$,也就是己未。這一年冬至是建子夏正十一月己未。
八節爲冬至、立春、春分、立夏、夏至、立秋、秋分、立冬。三統曆一年 $365 \frac{385}{1539}$ 日,每節平均長度爲 $365 \frac{385}{1539} \div 8 = 45 \frac{1010}{1539}$ 日。已知冬至大餘和冬至小餘,只要將它們分別加上每節長度就是八節各自的大餘和小餘。假設八節次序爲 $j$ (冬至爲 0),則第 $j$ 個八節的大餘、小餘可以用以下公式算出。
八節大餘:$$\text{冬至大餘} + 45 \times j$$ 八節小餘:$$\text{冬至小餘} + 1010 \times j$$
而每個節氣的長度是 $365 \frac{385}{1539} \div 24 = 15 \frac{1010}{4617}$。假設二十四節氣次序爲 $i$ (冬至爲 0),則第 $i$ 個二十四節氣的大餘、小餘可以用以下公式算出。因爲小餘以 4617 爲分母,而上面算出的冬至小餘是以 1539 爲分母的,所以這裏要先將冬至小餘乘以 3。
二十四節氣大餘:$$\text{冬至大餘} + 15 \times i$$ 二十四節氣小餘,以 $3 \times 1539 = 4617$ 爲分母(法):$$\text{冬至小餘} \times 3 + 1010 \times i$$
推五行
推五行,其四行各七十三日,統(歲)[法]分之七十七。中央各十八日,統法分之四百四。冬至後,中央二十七日六百六分。
三統曆把一年的日子按照五行木、火、土、金、水分爲五個部分。但是五行所屬的日子並不是一個接着一個的,也就是說,並不是屬木的日子結束之後立馬跟着屬火的日子。三統曆是把木、火、金、水分別和春夏秋冬四季搭配,而四季當中各有一部分日子屬於土,這叫做“土王四季”。
一年 $365 \frac{385}{1539}$ 日,平均分爲五行,每行 $365 \frac{385}{1539} \div 5 = 73 \frac{77}{1539}$ 日;其中屬土的日子要分爲四份,分別歸入四季,因此土日每份爲 $73 \frac{77}{1539} \div 4 = 18 \frac{404}{1539}$ 日。也就是對於春夏秋冬四季,每一季的前 $73 \frac{77}{1539}$ 日屬於各自季節相對應的五行,而每一季的後 $18 \frac{404}{1539}$ 日屬於土。這樣加起來,正好是一年的日子。春夏秋冬分別從立春、立夏、立秋、立冬開始。畫成圖更好理解。
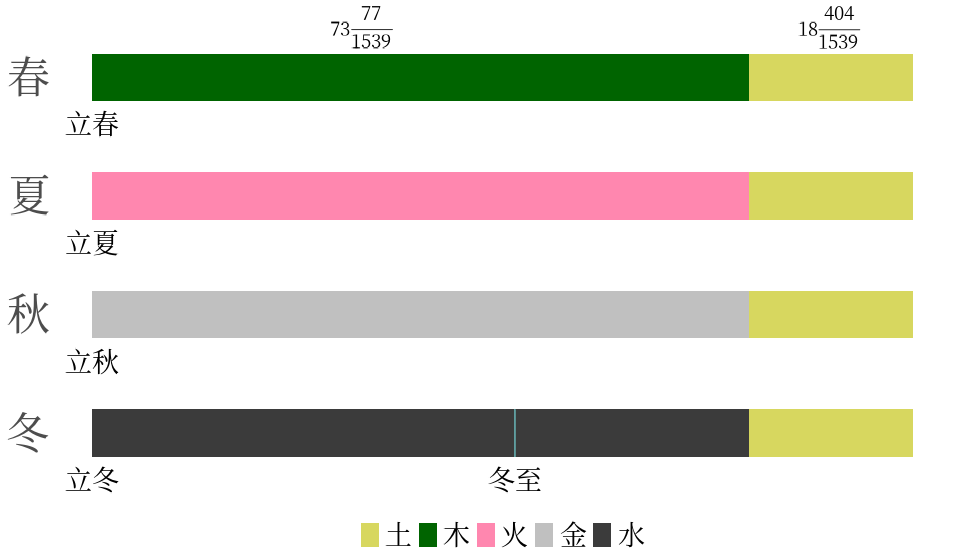
圖裏面,每個季節最後一段就是屬土的日子。冬季一段還標出了冬至的位置,就是圖中藍色豎線的地方。《律曆志》說“冬至後,中央二十七日六百六分”的意思是從冬至到冬季屬中央土的日子還有 $27 \frac{606}{1539}$ 日。這是因爲冬至距離立春還有小寒、大寒,加上冬至總共三個節氣,根據上一個部分,推八節的部分,三個節氣之間相距 $45 \frac{1010}{1539}$ 日,再減去冬至與立春之間中央土日 $18 \frac{404}{1539}$ 日,就是 $27 \frac{606}{1539}$ 日。
推合晨所在星
推合晨所在星,置積日,以統法乘之,以十九乘小餘而并之。盈周天,除去之;不盈者,令盈統法得一度。數起牽牛,算外,則合晨所入星度也。
這一段是求入統年天正月朔日的日月合朔所在星度。《左傳·昭公七年》伯瑕說:“日月之會是謂辰”,所以合晨度(晨通辰)就是日月合朔時刻的星度。太陽每天運行一度,一年 $365 \frac{385}{1539} = \frac{562120}{1539}$ 日,也就是太陽運行一週的度數。562120 就是以統法爲分母的周天度數。所以只要算出自統首至入統年正月朔日總共有多少天,也就是積日和積日小餘(不足一日的部分),就可以算出日月合朔時所在星度。
積日和積日小餘已經在推正月朔部分求出。設積日爲 $j$,積日小餘爲 $y$,周天 562120,先求不盈周天度數,這就是日月運行不足一個週期的數值。
$$ \begin{align*} &\text{積日} \frac{小餘}{81} \div (365 \frac{385}{1539})\\ =& \frac{81 j + y}{81} \div (\frac{562120}{1539})\\ =& \frac{(81j+y) \times 1539}{81 \times 562120}\\ =& \frac{(81j+y) \times 19}{562120}\\ =& \frac{1539j+19y}{562120}\\ =& (1539j+19y) \ \mathbf{div}\ 562120)\frac{(1539j+19y) \ \mathbf{mod}\ 562120}{562120}\\ \text{不盈周天度數}=&(1539j+19y) \ \mathbf{mod}\ 562120 \end{align*} $$
不盈周天度數是日月運行不足一個週期的數值,但是還要求這個度數相當於一年 $365 \frac{385}{1539}$ 度數的多少度,所以要除以統法 1539。下面就是三統曆求合晨度的最終公式:
$$ \begin{align*} \text{合晨度}&=\text{不盈周天度數}\div 1539\\ &=((1539j+19y) \ \mathbf{mod}\ 562120)\ \mathbf{div}\ 1539\frac{((1539j+19y) \ \mathbf{mod}\ 562120)\ \mathbf{mod}\ 1539}{1539} \end{align*} $$
由於三統曆的冬至點在牽牛初度,所以合晨度從牽牛初度起算。
寫成代碼:
def tuiHechen(jiri, xiaoyu):
hechendu = (jiri * 1539 + xiaoyu * 19) % 562120 // 1539 + 1
hechenXiaoyu = (dayu * 1539 + xiaoyu * 19) % 562120 % 1539
return hechendu, hechenXiaoyu
推其日夜半所在星
推其日夜半所在星,以章歲乘月小餘,以減合晨度。小餘不足者,破全度。
由於日月合朔不一定在夜半,所以求朔日夜半星度需要以合晨度(也就是日月合朔度數)減去夜半,也就是積日小餘,這裏叫做月小餘2。合晨度和合晨度小餘上一部分已經求出。設合晨度爲 $c$,合晨度小餘爲 $z$,積日小餘爲 $y$:
$$ \begin{align*} &\text{合晨度} \frac{合晨度小餘}{1539} - \frac{\text{積日小餘}}{81}\\ =&\text{c} \frac{z}{1539} - \frac{\text{y}\times 19}{1539}\\ =&\frac{1539c + z - 19c}{1539}\\ =&((1539c + z - 19c)\ \mathbf{div}\ 1539)\frac{(1539c + z - 19c)\ \mathbf{mod}\ 1539}{1539} \end{align*} $$
推其月夜半所在星
推其月夜半所在星,以月周乘月小餘,盈統法得一度,以減合晨度。
正因爲夜半並不一定是日月合朔時刻,所以日月並不一定同度,所以算了夜半太陽所在星度,還可以算夜半月亮所在星度。與上一部分求日夜半所在星一樣,只要以日月合朔星度,也就是合晨度減去夜半之後月行度數,就是夜半月亮所在的星度。
一章十九年,月亮有 254 個恆星月。注意,這裏的恆星月與朔望月不同。朔望月是月相變化的週期,而恆星月則是月球相對於一顆遙遠恆星的自傳週期,與地球上的恆星年相當。一章有 254 個恆星月,那每個恆星月以日爲單位的長度就是:
$$ \begin{align*} &\text{一章日數} \div \text{一章恆星月總數}\\ =&\frac{562120}{81} \div 254\\ =& \frac{562120}{81 \times 254} \end{align*} $$
周天總共 $\frac{562120}{1539}$ 度,所以月亮每日運行的度數就是:
$$ \begin{align*} &\text{周天度數} \div \text{一個恆星月日數}\\ =& \frac{562120}{1539} \div \frac{562120}{81 \times 254}\\ =& \frac{562120}{1539} \times \frac{81 \times 254}{562120}\\ =& \frac{81 \times 254}{1539}\\ =& \frac{254}{19} \end{align*} $$
以恆星月而言,月亮一日行 $\frac{254}{19}$ 度。所以求月亮夜半星度只要以日月合晨度數減去不足一日月行的度數,也就是積日小餘與恆星月日行度數的積,就能得到月所在星度。設積日小餘爲 $y$,夜半月亮所在星度就是:
$$ \begin{align*} \text{月夜半所在星度} &=\text{合晨度} \frac{合晨度小餘}{1539} - (\frac{\text{積日小餘}}{81} \times \frac{254}{19} )\\ &=\text{c} \frac{z}{1539} - \frac{\text{y}\times 254}{1539}\\ &=\frac{1539c + z - 254y}{1539}\\ &=((1539c + z - 254y)\ \mathbf{div}\ 1539)\frac{(1539c + z - 254y)\ \mathbf{mod}\ 1539}{1539} \end{align*} $$
推諸加時
推諸加時,以十二乘小餘為實,各盈分母為法,數起於子,算外,則所加辰也。
推諸加時的意思是以小餘計算各項數值在一天中的具體時刻。積日小餘是不足一日的部分,所以可以將積日小餘轉化成十二個時辰的時刻。三統曆將一日分爲十二時,所以將小餘乘以 12,化爲帶分數,整數部分就是時,而分數部分就是分。公式是:
$$ \begin{align*} \text{加時}&=\frac{12 \times 小餘}{各盈分母}\\ &=(12 \times 小餘 \ \mathbf{div}\ 各盈分母) \frac{12 \times 小餘 \ \mathbf{mod}\ 各盈分母}{各盈分母} \end{align*} $$
當然分數部分也能化爲六十進制的分秒。
推月食
推月食,置會餘歲積月,以二十三乘之,盈百三十五,除之。不盈者,加二十三得一月,盈百三十五,數所得,起其正,算外,則食月也。加時,在望日衝辰。
三統曆以 135 爲月食週期,135 個月會出現 23 次月食。但是一年平均 $12 \frac{7}{19} = \frac{235}{19}$ 個月,並不是 \frac{135}{23} 的整數倍。所以需要算出 月食週期與回歸年長度的最小公倍數。月食週期 135 月,一年平均 $\frac{235}{19}$ 月,135 和 235 的最小公倍數是 6345。這個最小公倍數叫做會月。一個會月是 6345 月,相當於 27 章 513 年。與會月相當的年數叫做會歲。寫成算式就是:
$$ \begin{align*} \text{會月} &= \mathbf{lcm}(\text{朔望之會}, \text{章月})\\ &=\mathbf{lcm}(135, 235)\\ &=6345\\ \text{會歲}&=(6345 \div \text{章月}) \times \text{章歲}\\ &=6345 \div 235 \times 19\\ &=513 \end{align*} $$
下一步是求會餘歲積月。本年自統首以來的積月已經在推天正部分求出了。設積月爲 $j$,$j$ 除以會月的餘數,$j \ \mathbf{mod}\ 6345$,就是會餘歲積月。因爲 135 個月有 23 次月食,所以每隔 $\frac{135}{23}$ 就有一次月食。所以根據三統曆算法的基本思路,要先算出會餘歲積月經過了幾個月食,也就是以會餘歲積月除以一個月食的週期:
$$ \begin{align*} \text{會餘歲積月} &=\text{積月} \ \mathbf{mod}\ \text{會歲}\\ &=j \ \mathbf{mod}\ 6345\\ &\text{會餘歲積月} \div \text{一個月食週期}\\ =&(j \ \mathbf{mod}\ 6345) \div \frac{135}{23}\\ =&(j \ \mathbf{mod}\ 6345) \times \frac{23}{135}\\ \text{食次}=&((j \ \mathbf{mod}\ 6345) \times 23) \ \mathbf{div}\ 135\\ \text{次餘}=&((j \ \mathbf{mod}\ 6345) \times 23) \ \mathbf{mod}\ 135\\ \end{align*} $$
食次爲會餘歲期間已經發生的日食數,而次餘就是本年天正月距離下一次月食的週期。假如次餘爲 0,則本年天正月就會發生月食。 而次餘與月食週期 135 的差值再除以 23 的商加一就是月食之月:
$$ \begin{align*} \text{當:次餘}+ 23 \times \text{月數} &\ge 135 \text{時,自天正月數相應月數就有月食}\\ \text{月食之月}&=(135-\text{次餘})\ \mathbf{div}\ 23 + 1 \end{align*} $$
歲術
推歲所在,置上元以來,外所求年,盈歲數,除去之,不盈者以百四十五乘之,以百四十四為法,如法得一,名曰積次,不盈者名曰次餘。積次盈十二,除去之,不盈者名曰定次。數從星紀起,算盡之外,則所在次也。欲知太歲,以六十除餘積次,餘不盈者,數從丙子起,算盡之外,則太歲日也。
推歲所在就是給定某年,求木星所在星次。木星的週期大約是十二年。春秋時就有用歲星所在星次來紀年的辦法。但是木星週期實際爲 11.86 年,所以三統曆發明了超辰法來計算歲星所在星次,並用來紀年。所謂超辰法,就是每過十二個木星週期,星次要往前進一個,跳過一個星次,所以叫做超辰法。設所求年距上元 $n$ 年,不盈歲數爲 $m$。
$$ \begin{align*} \text{歲星歲數}&= 144 \times 12\\ &=1728\\ \text{超辰}&=12 + 1 =13 \\ \text{不盈歲數}&=n \ \mathbf{mod}\ 1728 = m\\ \text{積次} \frac{次餘}{144}&= m \times \frac{145}{144}\\ &=(145m \ \mathbf{div}\ 144) \frac{145n \ \mathbf{div}\ 144}{144}\\ \text{積次}&=145m \ \mathbf{div}\ 144\\ \text{次餘}&=145m \ \mathbf{mod}\ 144\\ \text{歲星所在星次}&=\text{積次}\ \mathbf{mod}\ 12\\ &=145m \ \mathbf{div}\ 144 \ \mathbf{mod}\ 12 \end{align*} $$
這一段還有求太歲的辦法,就是積次除以六十的餘數,再以丙子爲起點,數出對應的干支。
$$\text{太歲} = \text{積次} \ \mathbf{mod}\ 60$$
